Policy Function and Value Function
The goal of the optimal policy function is to maximize the expected discounted reward, even if this means taking actions that would lead to lower immediate next-step rewards from few states. Recall that from the previous lecture that for all s, the (optimal) value function is:
![=\max {a}\left[\sum_{s^{\prime}} T\left(s, a, s^{\prime}\right)\left(R\left(s, a, s^{\prime}\right)+\gamma V^{*}\left(s^{\prime}\right)\right)\right]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-3004b334996fae62f211d38279320c39_l3.png "Rendered by QuickLaTeX.com")
where 
Estimating Transition Probabilities and Rewards
What might be some issue(s) with trying to estimate 
in the following manner?
![\[\begin{aligned}\hat{T} &=\frac{\operatorname{count}\left(s, a, s^{\prime}\right)}{\sum_{s^{\prime}} \operatorname{count}\left(s, a, s^{\prime}\right)} \\hat{R} &=\frac{\sum_{t=1}^{\operatorname{count}\left(s, a, s^{\prime}\right)} R_{t}\left(s, a, s^{\prime}\right)}{\operatorname{count}\left(s, a, s^{\prime}\right)}\end{aligned}\]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-de0985bef8597cdf44041b8a8f606dbb_l3.png "Rendered by QuickLaTeX.com")
- Certain states might not be visited at all while collecting the statistics for
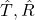
- Certain states might be visited much less often than others leading to very noisy estimates of
Model Free vs Model Based Approaches
Say we want to estimate the expectation of a function 
.
![\[\mathbb{E}[f(x)]=\sum_{x} p(x) \cdot f(x)\]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-6a6644abc21b63962dc0d5864c9d01bf_l3.png "Rendered by QuickLaTeX.com")
Model Based Approach works by sampling
points from the distribution 
and estimating, ![\[\hat{p}(X)=\frac{\operatorname{count}(x)}{K}\]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-989ed84457432ced579ce179bab51c26_l3.png "Rendered by QuickLaTeX.com")
before estimating the expectation of
as follows: ![\[E[f(X)] \approx \sum p(x) f(x)\]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-fb3901e9b9222f92ad643095597770ff_l3.png "Rendered by QuickLaTeX.com")
Model Free Approach would sample
points from and directly estimate the expectation of as follows: ![\[E[f(X)] \approx \frac{\sum_{i=1}^{K} f\left(X_{i}\right)}{K}\]](https://ayoubb.com/wp-content/ql-cache/quicklatex.com-1e340644b9713940c431070a004f814a_l3.png "Rendered by QuickLaTeX.com")
Exploration vs Exploitation
Examples of exploration:
- Try a new restaurant as opposed to going to your favorite one
- Play a random move in a game as opposed to playing the move that you believe is best
- Take a different path to work as opposed to the one that you believe is the fastest
Epsilon-Greedy Approach
Epsilon controls the exploration aspect of the RL algorithm: Higher the value of
, higher are the chances that the agent takes a random action during the learning phase and higher are the chances that it explores new states and actions. As the agent learns to act well, and has sufficiently explored its environment,
should be decayed off so that the value and Q function samples get less noisy with some of the randomness in the agent’s policy eliminated.
